適性検査傾向と対策 第3回 ~H28理系より
今回も長野県独特の「正解が1つしかない誘導型問題」について分析していきたいと思います。思考過程を制限しているのが特徴です。
第3回 比の活用問題
【例題】
直線ABは28m、直線BCは35mです。今、5年男子20人、5年女子24人、6年男子32人、6年女子36人が次のように並びます。
5、6年男子が太線上に、5、6年女子が外側の点線上に並ぶよう計画しました。AD、BC、EH、FGの直線上では、それぞれ12人が同じ間隔で並びます。残りの人は、内側と外側のカーブの部分で、すべて同じ間隔で並びます。このとき、直線AEの長さは何mですか。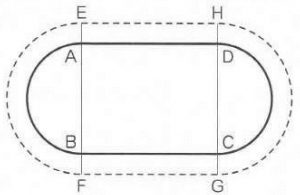
5、6年男子が太線上に、5、6年女子が外側の点線上に並ぶよう計画しました。AD、BC、EH、FGの直線上では、それぞれ12人が同じ間隔で並びます。残りの人は、内側と外側のカーブの部分で、すべて同じ間隔で並びます。このとき、直線AEの長さは何mですか。

【解説】
本問はこのあと以下のような誘導で解かせています。
誘導①太線のカーブと点線のカーブに並ぶ人数をそれぞれ求める
誘導②誘導①より、太線のカーブと点線のカーブの長さの比を求める
誘導③誘導②よりAEの長さを求める
誘導②誘導①より、太線のカーブと点線のカーブの長さの比を求める
誘導③誘導②よりAEの長さを求める
一見すると植木算の考え方を使いたくなる問題ですが、本問の狙いはそこではありません。実は間隔の長さを求めなくても、AEの長さは求められる、という点に主題があります。典型的な誘導型問題です。柔軟な思考が求められると言えるでしょう。
【解答例】
男子のカーブに並ぶ人数は
20+32-12×2=28 より28人
女子のカーブに並ぶ人数は
24+36-12×2=36 より36人
男女とも同じ間隔で並ぶことから、太線のカーブの長さと点線のカーブの長さの比は
28:36=7:9
より7:9になります。ここで円周の長さの比と直径の比は等しいので
7:9=28:□ より □=36 つまりEF=36m
(36-28)÷2=4 よってAE=4m
【対策について】
この問題のように、比を利用すると簡単に解ける問題は数多くあります。ですが、ふだんの学習ではなかなか気づきにくいものです。そこで、問題を解いていく際にふだんから「別の解き方はないかな」と考えるクセを身に付けさせましょう。また、答えを出した際に考え方を説明させて、その考え方に無駄な部分や遠回りしている部分がないか親御さんの方でチェックするのも有効です。少なくとも「答えさえ出ればいい」という考え方は適性検査には不利となることを早い段階で実感させる必要はあるでしょう。
■時習館の適性検査対策ゼミのご案内はコチラ