入試問題に挑戦！ 平成17年　宮城県　(超難)

平成17年度　宮城県立高校入試　数学

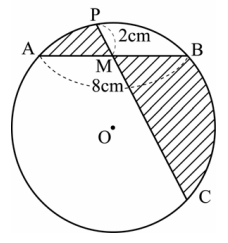　図のように、長さが 8cm の線分 AB があり、その中点を M とする。線分 AB 上にない点 P を PM=2cm になるようにとり、3 点 A、B、P を通る円を O とし、直線 PM と円 O との交点のうち P 以外の点を C とする。∠PMA＝60°のとき、斜線部分の面積を求めなさい。ただし､円周率はπとし､弧 AP､弧BCはともに小さい方の弧とする｡

↓

↓

↓

↓

↓

解説解答はコチラ

↓

↓

↓

↓

↓

↓

↓

↓

↓

↓

問６　（空間図形）

M は線分 AB の中点なので、AM=4cm となり、PM=2cm なので、AM:PM=1:2 となる。

ここで、AM:PM=1:2 かつ ∠PMA＝60° であれば、△APM は直角三角形になる。（線分比1:2:√3の三角形 ⇔ 角度30°,60°,90°の三角形） ゆえに、∠PMA＝60°、∠PAM＝30°、∠APM＝90° である。また、PM=2cm AM=4cm AP=2√3cm である。

同様に、△BCM は直角三角形になり、BM=4cm CM=8cm BC=4√3cm である。

次に円周上の点 PB に注目する。∠PAM＝30° なので、円周角∠PAB＝30° であり、中心角∠POB＝60° となる。（中心角は円周角の2倍になる）

また、円周上の点 AC に注目すると、円周角∠ABC＝90° なので、線分 AC は円の中心 O を通る直径となる。三平方の定理より線分 AC を求めると、線分 AC = √112 = 4√7cm になるので、円の半径は 2√7cm である。

弧 AP と線分 AP で囲まれる扇型の面積を S 、弧 BC と線分 BC で囲まれる扇型の面積を T とすると、求めるべき斜線部分の面積は、S　+　T　+　△APM　+ △BCM　である。

△APM の面積は、2√3c㎡、△APM の面積は、8√3c㎡ である。

次に S + T の面積を求める。S + T の面積は、半円 AOC の面積から、△AOPの面積・扇型POBの面積・△BOCの面積を引けばよい。

半円 AOC の面積は、半径 2√7cm なので、14πc㎡ となる。

△AOP は、線分AO = 線分PO = 半径2√7cm で、かつ底辺が2√3cm の二等辺三角形なので、面積は 5√3c㎡ になる。

<△BOC は、線分BO = 線分CO = 半径2√7cm で、かつ底辺が4√3cm の二等辺三角形なので、面積は 8√3c㎡ になる。/div>