ワカるデキる　対数（４）　～底を10にしてみる～

　以下の数字はだいたいいくつ？（有効数字２ケタで示せ）

6,013,279,453,781,418,791

　え～と、一、十、百、千、万、十万、百万、千万、一億、十億、百億、千億、一兆、十兆、百兆、千兆、一京、十京、百京、・・・ん～と、６００京ぐらいか？

　ただこういう数え方って面倒だし、示し方も科学的ではないよね。やはり科学的にはこう書いて欲しい。

　 $6.0\times10^{18}$

　科学では、桁数を表すのに “10” を底とした指数で表現することが大事になるのだ。

　ところで、前回までに以下のことを学習したね。

　「”2″ という底が “8”という数字（真数）になるのは、”3″乗した場合（対数）である」。

　これを数式で表すと、 $\log_2 8=3$ となったわけだ。

　でも、科学的には、”10″ を底とする対数を使うことが多い。たとえば、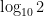 $\log_{10} 2$ とか $\log_{10} 3$ とかだ。このように、底を “10” にした対数を常用対数というんだ。ところで、 $\log_{10} 3$ ってどういう意味だ？　これは、「”10″ という底を、何乗（対数）かすると、”3″ という数字（真数）になる」てことだ。

　ん？　”10″ を、何乗かして、”3″ にする？　そんなことできるのか？　というと、できるのである。たとえば、”10″ の 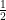$\frac{1}{2}$ 乗っていうのは、 $\sqrt{10}$ で、”3.1622″ で、”3″ にきわめて近い。つまり、 $\log_{10} 3$ は $\frac{1}{2}=0.5$ に近い数字だ。このように、計算していくと、”10″ を、何乗かして、”3″ になる数というのは必ず存在する。ただ、これは普通には計算できない。計算できなければどうするの？というと、これはだいたい数値として与えられるのだ。